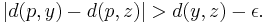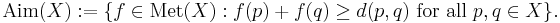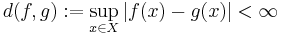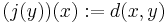Metric space aimed at its subspace
In mathematics, a metric space aimed at its subspace is a categorical construction that has a direct geometric meaning. It is also a useful step toward the construction of the metric envelope, or tight span, which are basic (injective) objects of the category of metric spaces.
Following (Holsztyński 1966), a notion of a metric space Y aimed at its subspace X is defined.
Informally, imagine terrain Y, and its part X, such that wherever in Y you place a sharpshooter, and an apple at another place in Y, and then let the sharpshooter fire, the bullet will go through the apple and will always hit a point of X, or at least it will fly arbitrarily close to points of X – then we say that Y is aimed at X.
A priori, it may seem plausible that for a given X the superspaces Y that aim at X can be arbitrarily large or at least huge. We will see that this is not the case. Among the spaces, which aim at a subspace isometric to X there is a unique (up to isometry) universal one, Aim(X), which in a sense of canonical isometric embeddings contains any other space aimed at (an isometric image of) X. And in the special case of an arbitrary compact metric space X every bounded subspace of an arbitrary metric space Y aimed at X is totally bounded (i.e. its metric completion is compact).
Definitions
Let 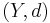 be a metric space. Let
be a metric space. Let  be a subset of
be a subset of  , so that
, so that 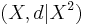 (the set
(the set  with the metric from
with the metric from  restricted to
restricted to  ) is a metric subspace of
) is a metric subspace of 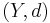 . Then
. Then
Definition. Space  aims at
aims at  if and only if, for all points
if and only if, for all points 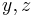 of
of  , and for every real
, and for every real 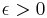 , there exists a point
, there exists a point  of
of  such that
such that
Let 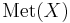 be the space of all real valued metric maps (non-contractive) of
be the space of all real valued metric maps (non-contractive) of  . Define
. Define
Then
for every 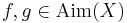 is a metric on
is a metric on 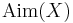 . Furthermore,
. Furthermore, 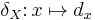 , where
, where 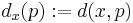 , is an isometric embedding of
, is an isometric embedding of  into
into 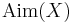 ; this is essentially a generalisation of the Kuratowski-Wojdysławski embedding of bounded metric spaces
; this is essentially a generalisation of the Kuratowski-Wojdysławski embedding of bounded metric spaces  into
into 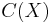 , where we here consider arbitrary metric spaces (bounded or unbounded). It is clear that the space
, where we here consider arbitrary metric spaces (bounded or unbounded). It is clear that the space 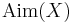 is aimed at
is aimed at 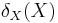 .
.
Properties
Let 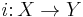 be an isometric embedding. Then there exists a natural metric map
be an isometric embedding. Then there exists a natural metric map 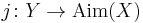 such that
such that 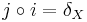 :
:
for every 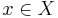 and
and 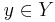 .
.
- Theorem The space Y above is aimed at subspace X if and only if the natural mapping
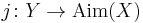 is an isometric embedding.
is an isometric embedding.
Thus it follows that every space aimed at X can be isometrically mapped into Aim(X), with some additional (essential) categorical requirements satisfied.
The space Aim(X) is injective (hyperconvex in the sense of Aronszajn-Panitchpakdi) – given a metric space M, which contains Aim(X) as a metric subspace, there is a canonical (and explicit) metric retraction of M onto Aim(X) (Holsztyński 1966).